Kuramoto - Generative Kunst
Philippe Lehmann
Kurzbeschreibung
Das Projekt Kuramoto zielt darauf ab, die Dynamik verschiedener mathematischer Modelle und komplexer Netzwerke auf künstlerischer Weise zu visualisieren. Diese Kunstform kann zur generativen Kunst zugeordnet werden, bei der der Entstehungsprozess eines Kunstwerkes eine zentrale Rolle spielt. Grundidee dieser künstlerischen Arbeit liegt in der automatisierten Ausführung von Regelabläufen, durch welche unvorhersehbare Gesamtgebilde und Formen entstehen.
Zu diesem Zweck implementieren wir nicht-lineare Differentialgleichungen eines gegebenen Modells numerisch, um sie mit computergestützten Näherungsmethoden zu lösen. Mathematische Modelle sind oft schwer zu verstehen, vor Allem dann wenn das mathematische Vorwissen fehlt. Die vorgestellten Visualisierungen zeigen den Lösungsraum der Modelle und helfen uns, eine Intuition für komplexe nichtlineare Differentialgleichungen aufzubauen. Auf diese Weise sind wir in der Lage die Mechanismen verschiedener Arten von Gleichungen visuel einzufangen. So wird unter Anderem ermöglicht ein künstlerisches Publikum auf wissenschaftliche Ergebnisse anzusprechen, zu denen es bislang kein Zugang gefunden hat.
Theorie
Ausgangspunkt dieser Arbeit ist ein mathematisches Modell, das die komplexen Interaktionen zwischen abstrakten Objekten, den so genannten „Kuramoto-Sakagushi-Oszillatoren“ simuliert. Diese Oszillatoren haben zwei Eigenschaften: sie besitzen eine Schwingungsfrequenz und eine Kopplungsstärke die sie zu weiteren Oszialltoren in ihrer Umgebung verbindet. Die programmgestützte Simulation löst die zugrunde liegenden Differentialgleichungen für die Frequenzen und Kopplungsstärken und gibt Lösungswerte zurück, die wir in einem weiteren Schritt visualisieren.
Dieses Modell stellt ein Netzwerk von allseits gekoppelten Kuramoto-Sakagushi-Oszillatoren latoren dar. Das bedeutet, dass jeder Oszillator mit jedem anderen Oszillator interagiert, indem sie ihre Frequenzen aneinander anpassen. Je stärker zwei Oszillatoren miteinander gekoppelt sind, desto schneller und wahrscheinlicher passen sich ihre Frequenzen an. Die linke Gleichung beschreibt die Frequenz dΦ/dt (die Änderung der Phase Φ i in der Zeit) des „i-ten“ von insgesamt N Oszillatoren. Man kann sehen, dass die Frequenz jedes Oszillators von der Kopplungsstärke „Kj“ mit jedem anderen Oszillator „j“ abhängt. Zu beachten ist dass die Summierung über „j“ stellvertretend für die Tatsache steht, dass die Wechselwirkungen von Oszillator i mit allen anderen Oszillatoren j aufaddiert werden. Das ωi weist jedem Oszillator die Anfangsfrequenz zu, während σ und α konstante Parameter darstellen. Die rechte Gleichung beschreibt die Änderungsrate der Kopplungsstärke Kj zwischen einem Oszillator einem benachbarten-Oszillator j. Auch hier sind σ und β konstante Parameter.
Prozess
Materialien:
• Python
• Libraries: Numpy, Matplotlib
Zur Lösung der Differentialgleichung verwenden wir einen numerischen Solver. Wir wählen Parameter und Anfangsbedingungen aus, welche aus verschiedenen wissenschaftlichen Publikationen bekannt, interessante Dynamiken mit Synchronisationseffekten erzeugen. Das Programm generiert eine Datei die wiederrum eine umfangreiche Matrix mit den Lösungen enthält. Wir rufen die Matrix auf und verbinden die Lösungspunkte mithilfe von der python library Matplotlib zu einer Vektorgrafik.
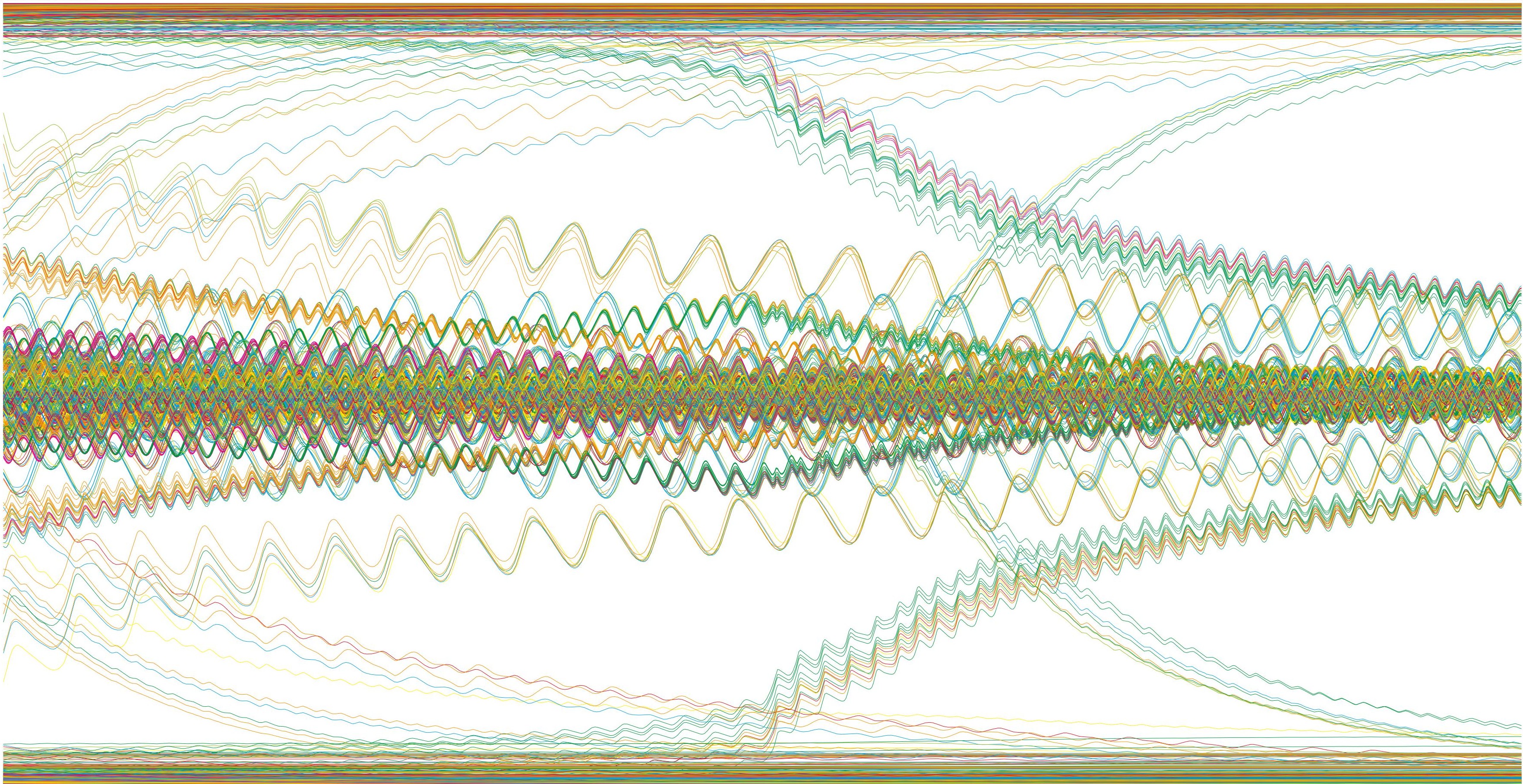
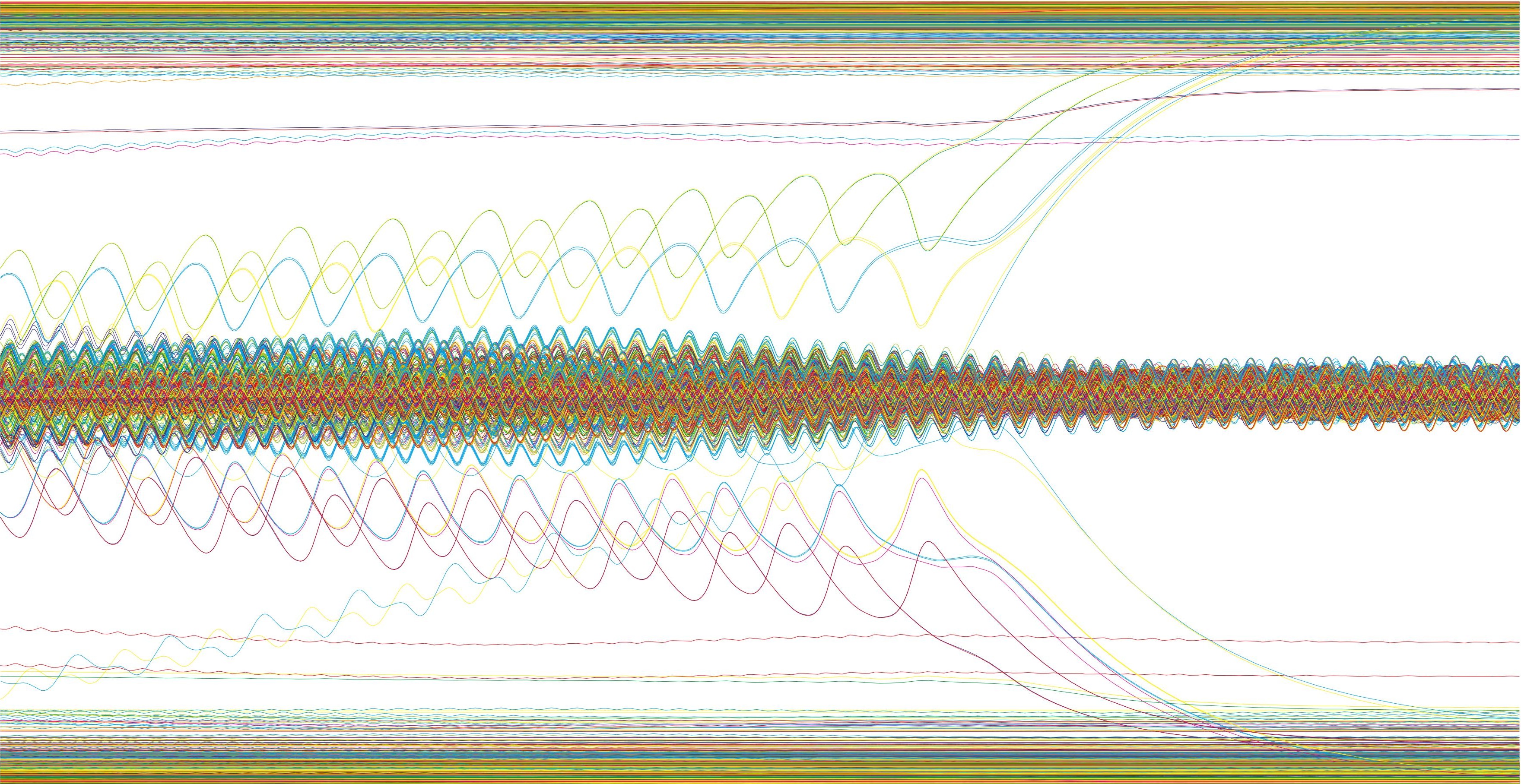
Plots
Fazit
Es ist wirklich erstaunlich wie aus einfachen Interaktionen zwischen den Oszillatoren derartig reiche und vielfältige Dynamiken entstehen. Jede Abbildung zeigt das Ergebnis für einen anderen Satz von Parametern. Zu sehen ist wie leicht unterschiedliche Parameter Eingaben zu völlig unterschiedlichen Mustern führen können. Auch ist deutlich erkennbar wie verschiedene Zufallsverteilungen dazu neigen sich zu verbinden sprich zu synchronisieren. Die Analogie zu natürlichen Phänomenen wie zB Fish und Vogel Schwarmverhalten ist nicht übersehbar: ein einfaches Regelverhalten der Netzwerkeinheiten führt zu einer kollektiven Frequenz.
Als nächsten Schritt werde ich weitere Parameter ausprobieren und Model Dynamiken visualisieren. Auch werde ich verschiedene Farbpaletten anlegen und mit transparenzen arbeiten um die Kontraste sowie Dichteverteilungen erkennbarer zu machen. Interessant wäre auch, die einzelnen Trajektorien mit ihrer Schwingungsfrequenz an einen Ton bzw eine hörbare Frequenz zu koppeln.