Dies ist eine alte Version des Dokuments!
Kurzbeschreibung
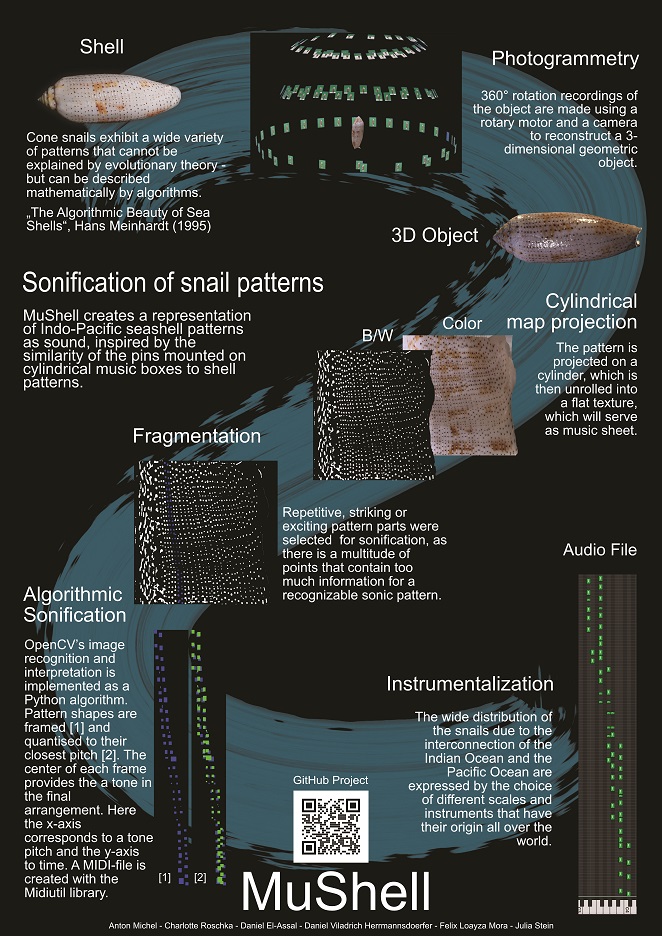
Die Inspiration für unser Projekt war die Ähnlichkeit einiger Kegelschnecken zu Walzenspieldosen. Die Punkte auf der Oberfläche des Gehäuses gleichen den Stiften auf der Walzenoberfläche auf verblüffende Weise. Daraus entstand die Kernfrage unseres Projektes: Wie kann man Muster aus der Natur hörbar machen?
Der Prozess, den wir zur “Verwandlung” der Schneckenschalen in Töne erarbeitet haben, beinhaltet Fotogrammetrie, um ein 3D Modell zu erstellen und als Flaches Bild darzustellen, Bildbearbeitung um die relevanten Muster zu extrahieren und weitere Datenverarbeitung in Python um diese Muster in bekannte MIDI-Dateien umzuwandeln, sowie die finale Instrumentalisierung der generierten MIDI Dateien in GarageBand.
Zur Präsentation des Projekts haben wir eigene Spieldosen gebaut. Diese drehen die Schnecke durch einen stepper Motor, der durch einen Arduino kontrolliert wird, während die Besucher die Vertonung des Musters durch Kopfhörer gespielt bekommen. Zusätzlich haben wir LEDs in der Spieldose montiert, die die erstellten Melodien periodisch wiedergeben.
 Abbildung 1: Aufbau der MuShell-Musicbox, Foto: Christel Clerc
Abbildung 1: Aufbau der MuShell-Musicbox, Foto: Christel Clerc
Theorie
Wie kommt die Vielfalt an Mustern in der Natur zustande?
In der Regel ist das Erscheinungsbild von Organismen eng mit einem evolutionären Wettbewerbsvorteil verknüpft.
Allerdings kann diese Maxime der Evolutionstheorie die Vielfalt an Mustern bei den oft sehr eng verwandten Kegelschnecken nicht erklären.
In seinem Buch „The algorithmic beauty of sea shells”, liefert Hans Meinhardt folgenden Erklärungsansatz: „[…] es ist anzunehmen, dass kein hoher selektionsdruck auf der Art des Musters liegt.
Die Vielfalt deutet darauf hin, dass das Muster drastisch verändert werden kann, ohne die Spezies zu bedrohen. Die Natur darf Spielen.“
 Abbildung 2: Schale einer c. textile.
Die parallelen dunkelbraunen Linien, in rot hervorgehoben, sind Resultat des Untergrund-Systems, welches Pigmente parallel zum Wachstumsrand (entlang der Ortskoordinate x) der Schale ablagert. Eine Störung dieses Systems führt zur Ausbildung der weißen Dreiecke entlang der Zeitkoordinate t.
Abbildung 2: Schale einer c. textile.
Die parallelen dunkelbraunen Linien, in rot hervorgehoben, sind Resultat des Untergrund-Systems, welches Pigmente parallel zum Wachstumsrand (entlang der Ortskoordinate x) der Schale ablagert. Eine Störung dieses Systems führt zur Ausbildung der weißen Dreiecke entlang der Zeitkoordinate t.
In grün hervorgehoben, sieht man, dass die parallelen Linien auch teilweise durch die weißen Dreiecke verlaufen, welches auf ein geschwächtes, aber nicht vollständig abgeschaltetes Untergrund-System hindeutet.
Von der Vielzahl an Mustern, die in dem Buch mathematisch beschrieben werden, möchten wir uns an dieser Stelle der conus textile widmen, da Sie eine der spannendsten Muster zeigt. Alle Kegelschnecken, zu denen auch c. textile gehört, haben gemeinsam, dass das Wachstum der Schale am Rand der Schalenöffnung stattfindet.
Der Prozess der Musterbildung ist somit sowohl ein orts- als auch zeitabhängiger Prozess (x, t).
Dies ist eine weitere Ähnlichkeit zu Walzenspieldosen, deren Melodie auch durch Orts- und Zeitkoordinaten bestimmt wird.
Wenn dann die Pigmentablagerung während des Schalenwachstums von mehreren oszillierenden Systemen bestimmt wird, bilden sich komplexe Muster.
Das Muster der c. textile speist sich aus einem kontinuierlichen Untergrund, welches die hellbraunen Flächen, sowie die dunkelbraunen parallelen Linien produziert (hervorgehoben in rot) und einem oszillierenden System, welches den Untergrund versorgt. Bricht die Versorgung des Untergrunds ab, etwa durch eine zu langsame Oszillation, setzt der Untergrund aus.
Es kommt zur Ausbildung der weißen Dreiecke.
In der grünen Box sieht man, dass der Untergrund auch bei geringer Versorgung parallele Linien ausbildet, allerdings ohne den hellbraunen Hintergrund.
Nicht ganz geklärt ist, welcher Mechanismus zum „restart“ des Untergrunds führt, da es sich wahrscheinlich um eine komplexe Verkettung unterschiedlicher Aktivator-Inhibitor Systeme handelt.
Für noch detailliertere Erläuterungen, sowie Anleitungen zur Simulation von Mustern empfiehlt sich die Lektüre des Buchs „The algorithmic beauty of sea shells“ von Hans Meinhardt.
Prozess
Schneckenauswahl
Zunächst haben wir geeignete Kegelschnecken (conus) ausgewählt, deren Schalen geeignete Muster aufweisen.
Dabei haben wir uns auf C. textile, C. arenatus, und C. nussatella geeinigt, da diese alle „Punktstrukturen“ zeigen, die sich gut mit unserem Python Algorithmus umsetzen lassen.
Die Schnecken sind in Abbildung 4 zu sehen.
Photogrammetrie (Agisoft Metashape)
Photogrammetrie ist ein Verfahren, in dem man Lage und Form eines Objekts durch das Zusammenfügen von Einzelaufnahmen in spezialisierten Programmen bestimmen kann. Ähnlich wie wir mit unseren Augen durch triangulation Räumlichkeit wahrnehmen können, vergleichen wir mit dem Programm Agisoft Metashape pro Schnecke zwischen 40 und 150 Fotos von verschiedenen Perspektiven aufgenommen, durch charakteristische Punkte, sogenannte Keypoints aus mehreren Fotos erkannt werden. die zusammen das 3D Modell der Schnecke erstellen.
Praktisch werden die Schnecken mithilfe einer Drehbühne rundum aus mehreren Winkeln fotografiert. Aus den Bildern wird ein 3D-Objekt mit der Textur der Schnecken erstellt.
Dabei ist es wichtig, Spiegelungen zu vermeiden und bei der Drehung der Schnecken einen gleichtönigen Hintergrund zu haben, damit die Keypoints nur die der Schnecke aus diesen verschiedenen Perspektiven sind.
Dieser Teil erfordert am meisten Rechenleistung, die daraus entstehende 3D Modelle können aber dann beliebig weiterverarbeitet werden und wurden auch frei verfügbar auf Sketchfab hochgeladen.
3D Modellierung und Projektion (Houdini und Blender)
Die 3D-Textur wird mittels zylindrischer Netzprojektion in eine 2D-Textur umgewandelt (Abbildung 3).
Dabei werden alle Schnecken in die gleiche horizontale Orientierung gebracht, sodass auch der Schnitt der Zylinder-projezierten Textur an der Lippe der Schnecke stattfindet, die keine Muster aufweist.
Es entsteht eine quadratische PNG-Bilddatei.
 Abbildung 3: 2-D Textur C. nussatella
Abbildung 3: 2-D Textur C. nussatella
Bildbearbeitung (GIMP)
Auf das Bild werden Filter wie Difference of Gaussians oder Sobel Edge detection angewandt, um die Punkt und Streifenmuster unabhängig von Ihrer Farbe und ohne kleineren Artefakten oder Verfärbungen hervorzuheben.
Dieses Bild wird dann mit der Threshold-Funktion in ein binäres Bild umgewandelt um einen maximal klaren Kontrast (schwarz-weiß) zu erhalten, der es dem Algorithmus erleichtert, die Konturen der Punkte zu erkennen.
Es werden interessante Teile des gesamten Musters ausgeschnitten, da das gesamte Muster zu viele Punkte (Noten) für einen klaren Klang enthält.


 \\Abbildung 4: Plakate der 3 Schnecken mit 3-D Modell, 2-D Textur (colored, S/W), farblich markierter Ausschnitt für Sonifizierung
\\Abbildung 4: Plakate der 3 Schnecken mit 3-D Modell, 2-D Textur (colored, S/W), farblich markierter Ausschnitt für Sonifizierung
Computer Vision (Python und openCV)
OpenCV ist eine Open-Source Bibliothek, die mehrere unterschiedliche computer vision (= computerbasiertes Sehen) Algorithmen enthält. Die in unserem Python Projekt verwendeten Algorithmen erlauben uns als Input Bilder zu bearbeiten, sowie Strukturen wie Punkte automatisch zu erkennen und eine Liste aller Punkte und ihrer Koordinaten zu erstellen, indem für jeden Punkt deren bounding box (umrahmende Box) erstellt wird.
Die x- und y-Koordinaten des Zentrums der Box werden jeweils als die Tonhöhe für an einem bestimmten Zeitpunkt der generierten Note übernommen.
Andere Eigenschaften wie zum Beispiel die vertikale Länge der Box bestimmen die Zeitdauer der jeweils generierten Note.
Anpassung an eine Tonleiter
Würde die Pixelkoordinaten des Bildes direkt als Noten übernommen werden, würden fast alle Noten von der geringen Anzahl an Noten innerhalb einer Tonleiter abweichen.
Wir wissen jedoch, dass verschiedene Kulturen mit Rücksicht auf Harmonisierung und andere akustische Effekte jeweils verschieden Tonleitern verwenden.
Durch eine Quantisierung der x- und y-Koordinaten werden die Tonhöhen der einzelnen Noten an einer Auswahl an Tonleitern angepasst und Akkorde mit der zeitlichen Quantisierung vermehrt.
In Anlehnung an die Weiterverbreitung von Kegelschnecken bedienen wir uns bei der Vertonung der Schnecken unterschiedlicher Tonleitern, die über das europäische heptatonische System hinausgehen. Ausgewählt wurden folgende Tonleitern:
- Balafon 1
- Asmaroneng Pelog
- Western A Major / Minor
- Arabic Rast on C
- Ionic
- Equal Temperament
MIDIutil
Die Tabellarisch aufgefassten Koordinaten der Punktmuster werden mit dem MIDIUtil Python Paket in eine MIDI datei umgewandelt.
GarageBand
Im letzten Schritt ist der größte Interpretationsspielraum enthalten, da wir die erhaltenen MIDI-Dateien in Garage Band nach unserem subjektiven Geschmack mit Instrumenten und Modulationen ausstatten.
Dabei haben wir Sowohl Traditionelle als auch moderne Synthetische Klänge benutzt, die das Muster der Muschel künstlerisch und pädagogisch am Besten wiedergeben können.
Bei feinen Mustern mit einer hohen Punktdichte eignen sich eher Staccato Klänge, bei gröberen Mustern eher fließende Töne.
Material
Für eine Musikbox mit LED strip (Abbildung 6)
- Stepper Motor 28BYJ-48 with driver
- Arduino Nano
- Protoboard 170
- 12 LED abschnitt WS2812B 144 LED per Meter
- 2x Male-to-male jumper cables
- 6x Male to female jumper cables
- 5V DC plug female
- 5-12 V power adapter
- Lötutensilien
Gestaltung Musicbox (Abbildung 7)
- Draht
- Thermoplastic
- Pappbox 12 cm breit
- Doppelseitiges Klebeband
- Sekundenkleber
- Schwarzer Sprühlack
- Klebeband
Gebaut nach Anleitung vom Tutorial: 28BYJ-48 STEPPER MOTOR WITH ULN2003 DRIVER - Arduino tutorial #14
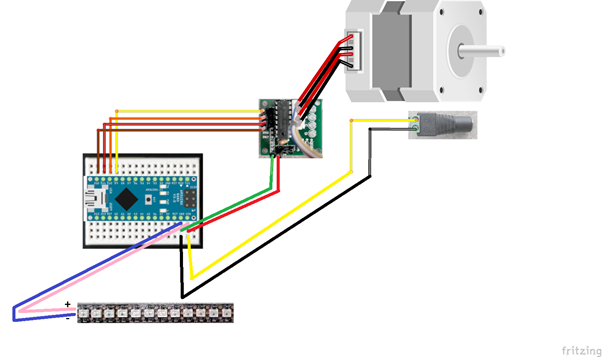 Abbildung 6: Arduino- und Schrittmotor-Verschaltung
Abbildung 6: Arduino- und Schrittmotor-Verschaltung
GitHub Link: https://github.com/dviladrich95/MuShell